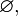Rabu, 29 Maret 2017

tip exel

Membuat Judul yang Tidak Gerak Jika Scroll Digeser Pada Ms.Excel 2007 2010(Freeze Pane)

Fitur Freeze Pane pada Ms Excel berfungsi untuk membiarkan beberapa bagian sel atau area kerja tetap terlihat atau diam sementara sel atau area sel yang lain dapat dilakukan scroll atau digerakkan. Freeze pane ini sangat membantu user untuk memasukkan data yang berupa tabel yang sangat panjang, mengingat jika dilakukan tanpa menggunakan fitur freeze pane, maka judul kolom tabel ataupun judul baris tidak akan terlihat sehingga menyulitkan user untuk memasukkan data.

Dibawah ini adalah langkah-langkah menggunakan fitur freeze panes di Ms Excel 2007.

Atur tapilan agar Kepala tabel terlihat dibagian atas dari area kerja ms excel.
Klik pada sel, dimana sel tersebut merupakan sel awal yang bisa discroll atau digerakkan. Artinya sel dalam deretan diatas dan dikiri sel terpilih tersebut yang akan dibekukan.
Klik Tab view kemudian pada group menu Windows klik Freeze Panes, lalu klik Freeze panes lagi. Jika anda pilih freeze top row, maka baris paling atas akan menjadi beku, sedangkan jika dipilih freeze first column maka kolom pertama yang akan dibekukan.
Mulai dari sekarang, ketika anda scroll kebawah atau atas maka area pink bagian atas tidak akan ikut bergerak sedangkan jika discroll kekanan maupun kekiri maka area pink sebelah kiri tidak akan ikut bergerak. Dengan demikian anda akan lebih mudah memasukkan data yang letaknya sangat jauh dari judul tabel.

Untuk menonaktifkan freeze panes atau mengembalikan pada kondisi awal, langkah yang dilakukan adalah klik tab view klik freeze panes dan pilih unfreeze panes, maka seluruh sel akan dapat discroll atau digerakkan.

Selasa, 28 Maret 2017

7 anggota badan yang harus dijaga dari maksiat & dosa

1. Mata - merupakan anugrah Allah yg harus digunakan tuk melihat sesuatu yg baik agar tk tersesat jalan. Oleh karna itu, jagalah mata dari 4 yg tercela, yaitu melihat perempuan yg bukan muhrim dgn penuh syahwat, melihat sesuatu yg menggairahkan nafsu birahi, melihat kpd sesama muslim dgn penuh kebencian & kesombongan, serta melihat kpd kaum muslimin dgn pandangan mengejek & menghinakan.

2. Telinga - alat pendengar anugrah Allah kpd kita, hendaknya digunakan untuk mendengar yg baik, jangan digunakan untuk mendengar omongan kotor, umpatan, & cela. Gunakan slalu untuk mendengarkan ayat-ayat Allah, & ilmu-ilmu hikmah oleh para alim ulama sehingga dapat mengecap & merasakan kebahagiaan yg kekal.

3. Lidah - alat penyambung hati untuk bicara, alat komunikasi antara seorang dgn yg orang lain. Hendaknya digunakan u tuk berzikir & membaca Alqur'an, mengajak sesama ummat manusia untuk taat & berbuat kebajikan.
Lidah bisa menimbulkan kekuatan bagi pemiliknya sekaligus pemusnah atau penghancur maka berhati-hatilah terhadapnya sebab : lidah dapat berdusta, dapat ingkar janji, dapat memfitnah, berbantah-bantahan soal agama & ketuhanan, lidah dapat memuji diri sendiri, menutuk atau mencela, bersenda gurau, mengejek, & mengolok.

4. Perut - tempat menyimpan makanan sebelum disebar ke seluruh anggota badan, sehingga kuat & dapat beribadah dengan tenang & khusu'.
Isilah perut dengan makanan atau sesuatu yg halal, baik zatnya,maupun cara mendapatkannya, janganlah diisi dgn yg haram.
Ingatlah sabda Rasulullah: "Setiap daging yg ditumbuhkan sebab dari sesuatu (makanan) yg haram, maka berhaklah dia menempati neraka".

5. Aurat ( kehormatan) termasuk anggota badan yg harus dijaga & dipelihara dari segala macam larangan Allah. Aurat pria .mulai pusar sampai lutut sedangkan wanita seluruh tubuh kecuali wajah & telapak tangan.

6. Tangan - hendaknya dijaga dari segala perbuatan tercela & dilarang agama misalnya untuk memukul sesama muslim, menerima harta yg haram (suap), jangan dipakai berkhianat, jangan dipake mencatat sesuatu yg takboleh diucapkan.

7. Kaki - hendaknya dipelihara dari segala macam langkah yg salah. Jangan dipake bepergian ketempat maksiat, jangan dipake bersegra menaati pimpinan yg dholim, karena sama menghinakan diri dihadapan mereka & menyanjung mereka dalam kedurhakaan

DARi https://plus.google.com/118253545432086213531/posts/YiW5p7eJt7V

Rabu, 22 Maret 2017

Keajaiban berbakti kepada orang tua

“Bersyukurlah (berterima kasihlah) kepada KU dan kepada orang tuamu, niscaya AKU akan menjagamu dari berbagai macam bencana, memanjangkan usiamu, menghidupkanmu dengan kehidupan yang baik dan membalikan keadaanmu kepada yang lebih baik dari sebelumnya”. (HR. Asakir, Jabira). “Barang siapa yang berbuat baik kepada orang tuanya, akan menjadilah ia sebagai orang yang paling baik dan akan dipanjangkan umurnya”. (HR Bukhori, Muslim).

Ajaran menghormati orang tua adalah ajaran universal, semua bangsa, semua budaya dan juga semua agama sepanjang sejarahnya selalu mengajarkan kepada kita agar berbakti kepada orang tua, karena mereka adalah orang yang sangat berjasa dalam hidup kita.

Berbakti kepada orang tua lebih utama dari jihad.

Banyak referensi yang memerintahkan kita berbakti baik kepada orang tua antara lain : “Bersyukurlah (berterima kasihlah) kepada KU dan kepada kedua orang tuamu, hanya kepada Aku tempat kembalimu” (QS, 31: 14).“Seorang anak tidak akan dapat membalas jasa orang tuanya, kecuali jika mendapati (orang tuanya) menjadi seorang hamba sahaya (budak) lalu ia membelinya kemudian memerdekakannya” (HR Muslim)
Bahkan dalam kasus tertentu berbakti kepada orang tua adalah lebih utama dari jihad : “Seseorang datang kepada Nabi SAW meminta izin untuk jihad. Nabi SAW bertanya; “apakah kedua orang tua mu masih hidup?” orang itu menjawab “ya”, maka nabi SAW bersabda “Hendaklah kamu berbakti kepada keduanya” (HR. Mukhari, Muslim).
Disebutkkan pula : “Pekerjaan yang paling disukai Allah adalah shalat tepat waktu, berbuat baik kepada Ibu Bapak dan setelah itu berjihad (berbuat baik) di jalan Allah” (Bukhari, Muslim).

Perintah untuk berbakti.

1. Berbakti kepada Allah dan orang tua. “Dan beribadahlah kepada Allah, janganlah kamu mempersekutukan-Nya dengan sesuatu apapun. Dan berbuat baiklah kepada kedua orang tua, kaum kerabat, anak-anak yatim, orang-orang miskin, tetangga dekat dan tetangga jauh, teman sejawat, ibnu sabil dan budak/pembantu yang kamu miliki, sungguh Allah tidak menyukai orang-orang yang sombong dan membanggakan diri’. (QS, 4:36)
2. Mengutamakan ibu / ibu mertua. “Dan Kami perintahkan kepada manusia berbuat baik kepada kedua orang tuanya, Ibunya telah mengandungnya dalam keadaan susah payah, dan melahirkan dengan susah payah (pula), masa mengandung sampai menyapihnya selama 30 bulan” (QS, 031:14).
“Wahai Rasul, kepada siapa aku berbuat kebaikan?”, beliau bersabda :”Ibumu”. Aku bertanya lagi : “Kemudian siapa?”, beliau bersabda : “Ibumu”. Aku bertanya lagi : “Kemudian siapa?”, beliau bersabda : “Ibumu”. Aku bertanya lagi : “Kemudian siapa lagi?”, beliau bersabda : “Ayahmu, lalu yang lebih dekat, kemudian yang lebih dekat (HR. Abu Dawud, At Tiirmizi).
Agama juga memerintahkan agar berbakti kepada mertua : “Ibu mertua kedudukannya sebagai ibu”. (HR. Tirmidzi dan Ahmad).
3. Memberikan nafkah kepada orang tua. “Apa saja harta yang kamu nafkahkan hendaklah diberikan kepada ibu-bapak, kaum kerabat, anak-anak yatim, orang-orang miskin dan orang-orang yang sedang dalam perjalanan. Dan apa saja kebajikan yang kamu buat, maka sesungguhnya Allah Maha Mengetahuinya”. (QS 2:215). “kamu dan hartamu adalah milik bapakmu (orang tuamu)” (HR. Ibu Majah).
4. Memelihara orang tua jika mereka lanjut usia. “Dan Tuhanmu telah memerintahkan supaya kamu jangan menyembah selain Dia (Allah) dan hendaklah kamu berbuat baik pada ibu bapakmu dengan sebaik-baiknya. Jika salah seorang di antara keduanya atau kedua-duanya sampai ber-umur lanjut dalam pemeliharaanmu, maka sekali-kali janganlah kamu mengatakan kepada keduanya perkataan “ah” dan janganlah kamu membentak mereka dan ucapkan-lah kepada mereka perkataan yang baik/mulia”.(QS,17:23).

Menyenangkan, jangan menyakiti orang tua.

“Aku akan bersumpah kepadamu untuk berhijrah dan aku tinggalkan orang tuaku dalam keadaan menangis”, Nabi SAW menjawab: “kembalilah kepada kedua orang tuamu dan buatlah mereka tertawa sebagaimana engkau telah membuatnya menangis”. (HR. Abu Dawud)
“Dan jika keduanya memaksamu untuk mempersekutukan Aku dengan dengan sesuatu yang kamu tidak mempunyai tentang itu, maka janganlah engkau mentaati keduanya, dan pergaulilah keduanya di dunia dengan baik, dan ikutilah jalan orang yang kembali kepada KU. Kemudian hanya kepada Ku lah tempat kembalimu, maka akan Aku beritahukan kepadamu apa yang telah kamu kerjakan (QS, Luqman :15)

Manfaat berbakti kepada orang tua.

1. Diridhai Allah : “Keridhaan (senang) Allah tergantung kepada keridhaan(senang) kedua orang tua dan murka Allah pun terletak pada murka kedua orang tua” (HR. Bukhori, Al Hakim).

2. Menjadi orang paling baik dan panjang umur : “Barang siapa yang berbuat baik kepada orang tuanya, akan menjadilah ia sebagai orang yang paling baik dan akan dipanjangkan umurnya”. (HR. Bukhori, Muslim)
3. Kehidupan menjadi lebih baik. “Bersyukurlah (berterima kasihlah) kepada KU dan kepada orang tuamu, niscaya AKU akan menjagamu dari berbagai macam bencana, memanjangkan usiamu, menghidupkanmu dengan kehidupan yang baik dan membalikan keadaanmu kepada yang lebih baik dari sebelumnya”. (HR. Asakir, Jabira)
4. Anak-anak kita juga akan berbakti : “Berbaktilah kepada Bapak dan Ibu supaya anak-anakmu berbakti kepadamu dan peliharalah dirimu dari perzinahan, supaya para istrimu memelihara dirinya”.(HR.Tabrani)

Bahaya melawan orang tua.

1. Memarahi orang tua sama dengan memarahi Allah : “Barang siapa orang yang merelakan diri kepada kedua orang tuanya, berarti ia rela (senang) kepada Allah. Dan siapa memarahi orang tua-nya, dia seperti memarahi Allah” ( HR Bukhori, Muslim)
2. Siksa / balasannya akan dipercepat di dunia.“Dua perbuatan dosa yang Allah cepatkan azabnya (siksanya) di dunia yakni : berbuat Zhalim dan durhaka kepada orang tua. “Semua bisa diampuni Allah jika Dia menghendaki, kecuali dosa durhaka kepada kedua orang tua (ayah dan ibu), Allah mempercepat balasan bagi durhaka tersebut di dunia sebelum mati”.(HR Bukhori, Muslim).
3. Dosa besar, bahkan dianggap kafir.“Janganlah kamu membenci ayah dan ibumu, maka siapa yang membenci kedua orang tuanya, ia telah berdosa (bahkan menjadi kafir)” (Bukhari, Muslim). “Hai Musa sesungguhnya satu satu kata dari orang yang durhaka terhadap orang tuanya, dosa-nya sama banyaknya dengan pasir yang ada di lautan”.(HR Abu Naim).
“Sesungguhnya Allah mengharamkan atas kamu durhaka kepada ibu, menolak kewajiban, minta sesuatu yang bukan haknya, dan membunuh anak hidup-hidup. Dan Allah membenci kamu banyak bicara, banyak bertanya (membantah), dan memboroskan harta (menghamburkan kekayaan)”. (HR Bukhari).
“Dosa besar yang paling besar yaitu; menyekutukan Allah, membunuh yang bernyawa, durhaka kepada ayah ibunya dan saksi palsu / berkata bohong”. (HR Bukhori, Muslim).
4. Tidak akan masuk surga. “Tidak akan masuk surga anak yang durhaka kepada orang tua, pecandu khamar (minuman keras), dan seorang yang mendustakan takdir“. (HR. Hasan)
“Ada tiga golongan yang tidak akan masuk surga dan Allah tidak mau melihat mereka pada hari Kiamat : (1) Anak yang durhaka kepada kedua orang tuanya, (2) perempuan yang menyerupai laki-laki dan (3) kepala rumah tangga yang membiarkan adanya kemungkaran (zina dll) dalam rumah tangganya” (HR Ahmad, Al Hakim).
5. Jangan saling mengutuk orang tua. Sesungguhnya dosa yang paling besar yaitu mengutuk kedua orang tuanya. Nabi ditanya, ”Ya Rasulullah, bagaimanakah kutukan seseorang terhadap kedua orang tuanya?” Nabi mengatakan, ”Yaitu memaki ayah dan ibu orang lain, lalu dibalasnya dengan memaki ayah dan ibu orang yang memaki tadi.’‘ (HR. Bukhari).

Ketika orang tua sudah tiada.

1. Memenuhi kewajiban, janji, pesan dll .“ Apakah masih ada yang ada yang harus saya lakukan untuk berbakti kepada kedua orang tuaku sesudah mereka tiada?“ Nabi menjawab: “ada”: yaitu berdoa dan beristigfar untuknya, memenuhi segala pesanan dan segala janji-janjinya dan menghubungi silaturahim yang harus dibuhubunginya, selanjutnya memuliakan teman-temannya” (Abu Daud, Ibnu Manjah, Ibnu Haban)
“Barang siapa yang meninggal dunia sementara dia memiliki kewajiban berpuasa, maka hendaknya walinya menggantikan puasanya” Aisyah. Saad: “Sesunggunya ibu telah meninggal dunia, sementara dia memiliki kewajiban nazar”, Rasulullah bersabda; “tunaikanlah nazar itu untuknya”.(HR Ibnu Abbas).
“Barangsiapa berhaji untuk kedua orang tuanya atau melunasi hutang-hutangnya maka dia akan dibangkitkan Allah pada hari kiamat dari golongan orang-orang yang mengamalkan kebajikan”. (HR. Ath-Thabrani, Ad-Daar Quthni).
2. Menjaga silahturahmi : “Jagalah selalu kecintaan ayahmu, janganlah engkau memutuskannya. Karena yang demikian Allah akan memadamkan cahaya darimu” (HR Bukhori, Muslim). “Sesungguhnya bakti yang paling baik(terhadap orang tua yang telah tiada) adalah seseorang menjalin hubungan dengan keluarga teman Bapaknya”. (Ibu Umar).
3. Bersedekah untuknya : “Ya Rosullah ibuku telah wafat sementara dia dia tidak berwasiat, jika aku bersedekah untuknya, apakah itu akan berguna baginya? Beliau menjawab “Ya”. (HR Ibnu Abbas).
4. Mendoakannya. “Tidak akan terputus rejeki seseorang selama dia tidak meninggalkan doa kepada orang tuanya dalam sehari. Dan sekiranya hamba itu meninggalkan do’a bagi kedua orang tuanya niscaya akan putus rezeki kepadanya”. (HR. Tabrani, Abu Yala, Al hakim) . “Sesungguhnya Allah akan mengangkat derajat hamba-nya yang saleh di surga, lalu si hamba berkata : wahai Tuhan, kenapa aku bisa mendapat derajat setinggi ini? Dijawab : karena istigfar dari anakmu” (HR. Ibnu Majah, Imam Malik).
5. Menghargai saudara yang lebih tua sebagai pengganti orang tua. “Kedudukan seorang paman sebagai (pengganti) kedudukan ayahnya”. (HR. Adarqothani). Kemudian “Abang yang tertua (sulung) kedudukannya sebagai ayah” (HR. Al-Baihaqi dan Ath-Thabrani)*.
Saat hari raya adalah saat yang tepat untuk memohon maaf, berterima kasih dan membahagiakan orang tua, semoga kita menjadi orang yang di ridhoi……
Ada ada baiknya kita ajak keluarga kita untuk berbakti kepada orang tua, “Barang siapa mengajak orang kepada kebaikan, maka dia akan mendapat pahala seperti pahala orang-orang yang mengikuti-nya tanpa mengurangi pahala mereka sedikitpun, barang siapa yang mengajak orang kepada keburukan, maka dia akan mendapatkan dosa seperti dosa orang yang mengikutinya, tanpa mengurangi dosa mereka sedikitpun“ (HR. Muslim).

http://www.thestraightway.info/thestraightway/keistimewaan-berbakti-kepada-orang-tua/

CARA MUDAH MENGHITUNG AKAR KUADRAT

LANGSUNG AJA DEH :d

sumbernya http://bestline99.blogspot.co.id

Kamis, 16 Maret 2017

http://matematika313.blogspot.co.id

VIDEO MENGETIK 10 JARI

CEKEDOT LINKNYA : https://www.youtube.com/watch?v=NpjczUgvZL4

Minggu, 12 Maret 2017

~Motivasi Belajar dari Imam Syafi'i~

"Jika Kamu tidak dapat menahan lelahnya belajar, | Maka kamu harus sanggup menahan perihnya Kebodohan."

~Imam Syafi'i~

Beliau rahimahullah berkata dalam kitab Diwan Al-Imam Asy-Syafi’i,

Aku melihat pemilik ilmu hidupnya mulia walau ia dilahirkan dari orangtua terhina.
Ia terus menerus menerus terangkat hingga pada derajat tinggi dan mulia.

Umat manusia mengikutinya dalam setiap keadaan laksana pengembala kambing ke sana sini diikuti hewan piaraan.
Jikalau tanpa ilmu umat manusia tidak akan merasa bahagia dan tidak mengenal halal dan haram.

Diantara keutamaan ilmu kepada penuntutnya adalah semua umat manusia dijadikan sebagai pelayannya.

Wajib menjaga ilmu laksana orang menjaga harga diri dan kehormatannya.
Siapa yang mengemban ilmu kemudian ia titipkan kepada orang yang bukan ahlinya karena kebodohannya maka ia akan mendzoliminya.

Wahai saudaraku, ilmu tidak akan diraih kecuali dengan enam syarat dan akan aku ceritakan perinciannya dibawah ini:
Cerdik, perhatian tinggi, sungguh-sungguh, bekal, dengan bimbingan guru dan panjangnya masa.

Setiap ilmu selain Al-Qur’an melalaikan diri kecuali ilmu hadits dan fikih dalam beragama.

Ilmu adalah yang berdasarkan riwayat dan sanad maka selain itu hanya was-was setan.

Bersabarlah terhadap kerasnya sikap seorang guru.
Sesungguhnya gagalnya mempelajari ilmu karena memusuhinya.

Barangsiapa belum merasakan pahitnya belajar walau sebentar,
Ia akan merasakan hinanya kebodohan sepanjang hidupnya.

Dan barangsiapa ketinggalan belajar di masa mudanya,
Maka bertakbirlah untuknya empat kali karena kematiannya.

Demi Allah hakekat seorang pemuda adalah dengan ilmu dan takwa.
Bila keduanya tidak ada maka tidak ada anggapan baginya.

Ilmu adalah tanaman kebanggaan maka hendaklah Anda bangga dengannya. Dan berhati-hatilah bila kebanggaan itu terlewatkan darimu.

Ketahuilah ilmu tidak akan didapat oleh orang yang pikirannya tercurah pada makanan dan pakaian
.
Pengagum ilmu akan selalu berusaha baik dalam keadaan telanjang dan berpakaian.

Jadikanlah bagi dirimu bagian yang cukup dan tinggalkan nikmatnya tidur
Mungkin suatu hari kamu hadir di suatu majelis menjadi tokoh besar di tempat majelsi itu.

***
Disadur dari kitab Kaifa Turabbi Waladan Shalihan (Terj. Begini Seharusnya Mendidik Anak), Al-Maghrbi bin As-Said Al-Maghribi, Darul Haq.
Artikel Muslimah.or.id

http://www.designdakwah.com/2014/08/motivasi-belajar-dari-imam-syafii.html

ISTIQFAR

Segala puji bagi Allâh, Rabb semesta alam. Shalawat dan salam atas Rasul-Nya yang terpercaya, keluarga, para shahabat serta orang yang mengikuti beliau hingga hari Kiamat, wa ba’du:
Berikut ini kami ketengahkan beberapa bahasan secara ringkas mengenai “Istighfar: keutamaan, waktu dan lafazhnya”. Kami memohon kepada Allâh agar menjadikan tulisan ini bermanfa’at.

I. Keutamaannya

Ia merupakan bentuk keta’atan kepada Allâh ‘Azza Wa Jalla
Istighfar merupakan sebab untuk diampuninya dosa, sebab turunnya hujan, mendapatkan harta dan anak serta masuknya manusia ke dalam surga. Nabi Nuh berkata ketika mendakwahi kaumnya, sebagimana firman Allah (artinya): “Maka aku katakan kepada mereka, ‘Mohonlah ampun kepada Rabbmu, sesungguhnya Dia adalah Maha Pengampun. Dia akan mengirimkan hujan kepadamu dengan lebat. Dan membanyakkan harta dan anak-anakmu, dan mengadakan untukmu kebun-kebun dan mengadakan (pula di dalamnya) untukmu sungai-sungai.” (Q.s. Nûh:10-12)
Kekuatan menjadi bertambah dengan istighfar, Allah Ta’ala berfirman (artinya), Dan (Hud berkata):“Hai kaumku, mohonlah ampun kepada Rabbmu lalu tobatlah kepada-Nya, niscaya Dia menurunkan hujan yang sangat deras atasmu, dan Dia akan menambahkan kekuatan kepada kekuatanmu, dan janganlah kamu berpaling dengan berbuat dosa”.(Q.s.Hûd:52)
Ia merupakan sebab mendapatkan kesenangan yang baik, serta menjadi sebab masing-masing orang yang memiliki keutamaan berhak mendapatkan keutamaannya. Allah Ta’ala berfirman (artinya), “Dan hendaklah kamu meminta ampun kepada Rabbmu dan bertaubat kepada-Nya. (Jika kamu mengerjakan yang demikian), niscaya Dia akan memberi kenikmatan yang baik (terus-menerus) kepadamu sampai kepada waktu yang telah ditentukan dan Dia akan memberi kepada tiap-tiap orang yang mempunyai keutamaan (balasan) keutamaannya.” (Q.,s.Hûd:3).
Allah tidak akan mengazab orang yang selalu beristighfar. Dia telah berfirman (artinya), “Dan tidaklah (pula) Allah akan mengazab mereka, sedang mereka meminta ampun.” (Q.s.al-Anfâl:33)
Ia dibutuhkan oleh hamba-hamba Allâh karena mereka selalu berbuat kesalahan sepanjang malam dan siang hari. Jadi, bila mereka beristighfar, Allâh pasti mengampuni mereka.
Rahmat akan turun dengan sebab istighfar. Allah Ta’ala berfirman, “Hendaklah kamu meminta ampun kepada Allah, agar kamu mendapat rahmat.”(Q.s.an-Naml:46)
Istighfar merupakan kaffarat (penebus dosa) yang dilakukan dalam suatu majlis.
Melakukannya berarti meneladani Nabi Shallallâhu ‘alaihi wasallam sebab beliau beristighfar di dalam satu majlis sebanyak 70 kali. Dalam riwayat yang lain disebutkan, sebanyak 100 kali.

II. Beberapa Ungkapan Mengenai Istighfar

Diriwayatkan dari Luqman ‘alaihissalâm bahwa dia berpesan kepada anaknya, “Wahai anakku! Biasakanlah lisanmu mengucapkan:
الَّلهُمَّ اغْفِرْ لِي
“Ya Allâh! ampunilah aku”, sebab Allâh menyediakan waktu-waktu dimana Dia Ta’âla tidak menolak doa orang yang berdoa kepada-Nya.”
‘Aisyah radhiallaahu ‘anha berkata, “Beruntunglah orang yang mendapatkan di dalam shahîfah (lembaran amalnya) istighfar yang banyak.”
Qatâdah berkata, “Sesungguhnya al-Qur’an ini menunjukkan kepada kalian penyakit dan obat; penyakit itu adalah dosa-dosa sedangkan obatnya adalah istighfar.”
Abu al-Minhâl berkata, “Tidak ada tetangga (teman dekat) yang lebih dicintai oleh seorang hamba kelak di kuburnya selain istighfar.”
al-Hasan berkata, “Perbanyaklah istighfar di rumah-rumah kalian, di hadapan hidangan-hidangan, di jalan-jalan, pasar-pasar serta majlis-majlis sebab kalian tidak tahu kapan ampunan-Nya akan turun.”
Seorang Arab Badui (orang yang biasa hidup di pedalaman gurun pasir) bertutur, “Barangsiapa yang mendiami bumi kami ini, maka hendaklah dia memperbanyak istighfar sebab bersama istighfar itulah terdapat awan tebal yang membawa curahan hujan.” (maksudnya istighfar itu merupakan sebab turunnya hujan-penj.,)

III. Waktu-waktu BeristighfarIstighfar disyari’atkan di dalam setiap waktu, tetapi ia menjadi wajib ketika melakukan dosa-dosa dan menjadi sunnah/sangat dianjurkan seusai melakukan perbuatan-perbuatan baik, seperti beristighfar 3 kali setelah shalat, setelah haji dan lain-lain.
Juga, dianjurkan pada waktu sahur sebab Allâh memuji orang-orang yang beristighfar pada waktu-waktu sahur tersebut.
IV. Lafazh-lafazh Istighfar

Lafazh paling utamanya adalah yang dikenal dengan Sayyidul Istighfar (penghulu istighfar), yaitu mengucapkan:
اللَّهُمَّ أَنْتَ رَبِّي لاَ إِلَهَ إِلاَّ أَنْتَ خَلَقْتَنِي وَأَنَا عَبْدُكَ وَأَنَا عَلَى عَهْدِكَ وَوَعْدِكَ مَااسْتَطَعْتُ أَعُوْذُُ بِكَ مِنْ شَرِّ مَا صَنَعْتُ أَبُوْءُ لَكَ بِنِعْمَتِكَ عَلَيَّ وَأَبُوْءُ بِذَنْبِي فَاغْفِرْلِي فَإِنَّهُ لاَ يَغْفِرُ الذُّنُوْبَ إِلاَّ أَنْتَ
“Ya Allâh! Engkaulah Rabbku, tiada Tuhan (yang berhak disembah) selain-Mu, Engkaulah Yang menciptakanku, dan aku adalah hamba-Mu, aku berada diatas ikatan dan janji-Mu selama aku mampu, aku berlindung kepada-Mu dari kejahatan yang aku buat, aku mengakui kepada-Mu atas nikmat-Mu kepadaku, dan aku juga mengakui kepada-Mu dosa-dosaku; maka ampunilah aku karena sesungguhnya tidak ada yang dapat mengampuni dosa-dosa selain Engkau”
Lafazh: أَسْتَغْفِر ُاللهَ
Lafazh: رَبِّ اغْفِرْ لِي
Lafazh: اللَّهُمَّ إِنِّي ظَلَمْتُ نَفْسِي فَاغْفِرْ لِي ؛ فَإِنَّهُ لاَ يَغْفِرُ الذُّنُوْبَ إِلاَّ أَنْتَ
“Ya Allâh! sesungguhnya aku telah menzhalimi diriku, maka ampunilah aku; karena sesungguhnya tidak ada yang dapat mengampuni dosa-dosa selain Engkau”
Lafazh: رَبِّ اغْفِرْ لِي وَتُبْ عَلَيَّ إِنَّكَ أَنْتَ التَّوَّابُ اْلغَفُوْرُ، أو التَّوَّابُ الرَّحِيْمُ“Tuhanku! Ampunilah aku dan berilah taubat kepadaku, sesungguhnya Engkaulah Maha Penerima taubat lagi Maha Pengampun, (atau )Maha Penerima taubat lagi Maha Pengasih”
Ucapan: اللَّهُمَّ إِنِّي ظَلَمْتُ نَفْسِي ظُلْمًا كَثِيْرًا وَلاَ يَغْفِرُ الذُّنُوْبَ إِلاَّ اللهَ، فَاغْفِرْ لِي مَغْفِرَةً مِنْ عِنْدِكَ، وَارْحَمْنِي إِنَّكَ أَنْتَ اْلغَفُوْرُ الرَّحِيْمُ“Ya Allâh! sesungguhnya aku telah menzhalimi diriku dengan kezhaliman yang banyak dan tidak ada Yang dapat mengampuni dosa-dosa selain Allâh, maka ampunilah aku dengan ampunan dari sisi-Mu, dan kasihilah aku, sesungguhnya Engkau-lah Yang Maha Pengampun lagi Maha Pengasih”
Ucapan:
أَسْتَغْفِرُ اللهَ َالَّذِي لاَ إِلَهَ إِلاَّ هُوَ اْلحَيُّ اْلقَيُّوْمُ وَأَتُوْبُ إِلَيْهِ“Aku memohon ampun kepada Allâh Yang tidak ada Tuhan (Yang berhak disembah) selain Dia Yang Maha Hidup Lagi Maha berdiri sendiri, dan aku bertaubat kepada-Nya”
وَصَلَّى للهُ عَلَى نَبِيِّنَا مُحَمَّدٍ وَعَلَى آلِهِ وَصَحْبِهِ وَسَلَّمْ

(Diambil dari artikel berjudul “al-Istighfâr: Fadlâ`iluh, Awqâtuh, Shiyaghuh” karya Muhammad bin Ibrahim al-Hamd oleh Abu Shofiyyah)
Sumber : http://tinyurl.com/istighfarlah

Sumber: https://aslibumiayu.net/5982-lafadz-lafadz-istighfar-yang-bisa-digunakan-untuk-beristighfar.html

kewajiban anak terhadap ibu bapak

kewajiban anak terhadap ibu bapak :

1.tidak berkata ah, / kasar , memahari tapi sebaliknya menyayangi
2.mendokan diwktu solat , wajib
3.memberikan hasil kerja keras semampunya, yang terbaik

sketsa

Home » Himpunan Semesta » Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian

Home » Himpunan Semesta » Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian

Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian

Himpunan Semesta dan Himpunan Bagian

Sebelum mempelajari himpunan semesta dan himpunan bagian , maka terlebih dahulu mempelajari himpunan bilangan , perhatikan penjelasan di bawah ini .

Himpunan Bilangan meliputi :

a. Himpunan Bilangan Asli ( A )

A = { 1 , 2 , 3 , 4 , . . . . }

Himpuna semesta

Himpunan semesta yaitu himpunan yang memuat semua anggota yang sedang dibicarakan . Himpunan semesta dilambangkan dengan huruf ” S ” .

Contoh 1 :

A = { 1 , 2, 3 , 5 , 7 }

B = { 5 , 7 , 9 }

S = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }

Irisan Himpunan ( $\cap$ )

Irisan Himpunan , dimisalkan A $\cap$ B yang artinya bahwa himpunan yang anggotanya menjadi nggota A , dan sekaligus menjadi anggota B .

Contoh 2:

A = { 1, 2 ,3 , 4 }

B= { 3 , 4 , 5 }

A $\cap$ B = { 3 , 4 }

Gabungan ( $\cup$ )

Gabungan , dimisalkan A $\cup$ B Yang artinya bahwa himpunan yang anggotanya menjadi anggota A atau menjadi anggota B .

Contoh 3:

A = { 1, 2 ,3 , 4 }

B= { 3 , 4 , 5 }

A $\cup$ B = { 1, 2 , 3 , 4 , 5 }

Diagram Venn

Suatu himpunan dapat dinyatakan dalam diagram ven , diagram ven merupakan diagram yang pertama kali dikemukakan oleh ilmuwan asal Inggris yang bernama JHON VENN .

Dalam diagram venn , himpuan semesta dinyatakan dengan benuk persegi panjang . Sedangkan himpunan yang lain , di luar semesta dinyatakan dalam kurva sederhana dan noktah – noktah untuk menyatakan anggotanya . Dan apabila tidak ada himpunan yang sama antara himpuna A dan B , maka lingkaran dalam himpunan semesta tersebut tidak saling berpotongan . Untuk lebih jelasnya perhatikan contoh di bawah ini

Contoh 4 :

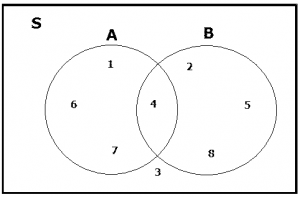
1.) S = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 }

A = { 1 , 4 , 6 , 7 }

B = { 2 , 4 , 5 , 8 }

A $\cap$ B = { 4 }

A $\cup$ B = { 1 , 2 , 4 , 5 , 6 , 7 , 8 }

Maka apabila digambarkan dalam diagram VENN , adalah :

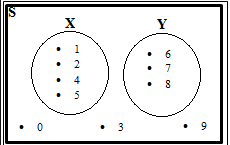
2.) S = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }

X = { 1, 2 , 4 , 5 }

Y = { 6 , 7 , 8 }

Himpunan Kosong ( { } )

Himpunan kosong adalah himpunan yang tidak memiliki anggota , dan dinotasikan dengan { } atau

\varnothing,

Himpunan kosong ( { } ) , merupakan himpunan bagian dari setiap himpunan .

Himpunan Bagian ( ⊂ )

Himpuna bagian dimisalkan dengan A ⊂ B , Artinya jika setiap anggota A ( Semua anggota A ) , Menjadi anggota B .

Contoh 5:

1.) A = { 1 , 2 , 3 }

B = { 0 , 1 ,2 , 3 , 4 }

A ⊂ B , Karena semua anggota A Menjadi anggota B .

2.) P = { a , b , c }

Q = { a , c , d , e , f }

P bukan Himpunan bagian dari Q ( P ⊂ Q ) , Karena ada anggota P yang tidak menjadi anggota Q .

3.) P = { a , b , c } , Tulislah semua himpunan bagian dari P

{ }
{ a }
{ b }
{ c }
{ a , b }
{ a , c }
{ b , c }
{ a , b , c }

“Catatan : Setiap himpunan , merupakan himpunan bagian dari himpunan itu sendiri “

Dari contoh nomor 3 , maka Cara untuk menentukan Banyaknya Himpunan Bagian A , maka Rumusnya adalah :

A = 2 ^n(A)

Keterangan :

n(A ) = Banyaknya anggota A

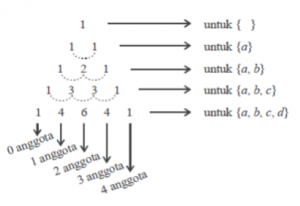
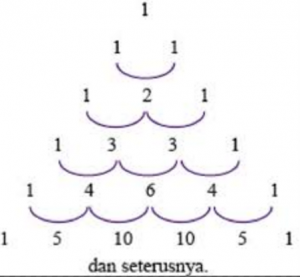
Untuk menentukan banyaknya himpunan bagian suatu himpunan ,yaitu dengan menggunakan konsep segitiga pascal . Perhatikan gambar di bawah ini :

4.) P ={ 0 , 1 , 2 , 3 , 4 } , n ( P ) = 5

a. Tentukan banyaknya himpunan bagian P

b. Tentukan Banyaknya Himpunan Bagian P yang mempunyai 3 anggota .

Penyelesaian :

a. Banyaknya Himpunan Bag. P = 2 ^n(P)

= 2 ⁵= 32

b. Banyaknya Himpunan Bagian P yang mempunyai 3 anggota adalah 10 ( caranya melihat segitiga pascal berikut)

Komplemen Suatu Himpunan

Komplemen suatu himpunan Dimisalkan dengan A^Catau A^l, yaitu himpunan yang anggotanya adalah anggota S selain anggota A

Untuk lebih memahaminya , perhatikan contoh berikut

Contoh 6 :

1.) S = { 0 ,1 ,2 ,3 ,4 ,5 }

A = { 1 , 2 , 3 , 4 }

Maka dihasilkan A^C= { 0 , 5 } dan ( A^C)^C= { 1 , 2 , 3 , 4 }

atau dengan kata lain ( A^C)^C= A

2.) S = { 0 , 1 , 2 ,3 ,4 , 5 , 6 , 7 , 8 , 9 }

P = { 2 , 3 , 4 , 5 }

Q = { 4 , 5 , 6 , 7 , 8 }

Tentukan :

a. P $\cap$ Q

b. P $\cup$ Q

c. P^C

d. Q^C

e. ( P $\cap$ Q )^C

f. ( P $\cup$ Q )^C

g. P^C $\cap$ Q^C

h. P^C $\cup$ Q^C

Penyelesaian :

a. P $\cap$ Q = { 4 , 5 }

b. P $\cup$ Q = { 2 , 3 , 4 , 5 , 6 , 7 , 8 }

c. P^C= { 0 , 1 , 6 , 7 , 8 , 9 }

d. Q^C= { 0 , 1 , 2 , 3 , 9 }

e. ( P $\cap$ Q )^C= { 0 , 1 , 2 , 3 , 6 , 7 , 8 , 9 }

f. ( P $\cup$ Q )^C= { 0 , 1 , 9 }

g. P^C $\cap$ Q^C= { 0 , 1 , 9 }

h. P^C $\cup$ Q^C= { 0 , 1 , 2 , 3 , 6 , 7 , 8 , 9 }

Dari Contoh di atas maka , dihaslkan rumus sebagai berikut :

( P   $\cap$   Q )^C= P^C $\cup$ Q^C
( P   $\cup$ Q )^C=   P^C $\cap$ Q^C
atau
( A   $\cap$   B )^C=A^C $\cup$ B^C
( A   $\cup$ B )^C=  A^C $\cap$ B^C

Demikian penjelasan mengenai Cara cepat untuk memahami Himpunan Semesta Dan Himpunan Bagian Dari suatu bilangan dalam ilmu matematika . Semoga dengan penjelasan di atas , dapat membantu anda dalam mengerjakan soal himpunan dan semua yang masalah yang termasuk di dalamnya . Semoga ilmu kita bermanfaat . Amin

http://rumusrumus.com/himpunan-semesta/

Pengertian, Teori, Konsep dan Jenis Himpunan Matematika

Rumus matematika - Himpunan matematika dapat didefinisikan sebagai sebuah kumpulan dari beberapa objek baik itu benda abstrak maupun benda real (nyata) yang dapat didefinisikan dengan jelas. Artinya benda-benda tersebut jelas adanya dan memiliki keterangan yang jelas. Salah satu contoh himpunan adalah kumpulan mahasiswa jurusan matematika FMIPA Universitas Lampung atau Kumpulan siswa kelas 6 SD Pelita Harapan. Intinya kumpulan tersebut didefinisikan dengan jelas. Berbeda dengan kumpulan anak yang berambut gondrong atau kumpulan anak-anak pandai, itu tidak bisa disebut himpunan karena benda-benda tersebut tidak didefinisikan dengan jelas dan tidak merujuk pada objek tertentu yang jelas keberadaannya.

Source: Google Images

Untuk mengetahui lebih jauh mengenai himpunan dalam matematika, simak pembahasan di bawah ini:

Pengertian, Teori, Konsep dan Jenis Himpunan Matematika

Notasi Himpunan

sebuah himpunan biasanya dinyatakan dengan simbol simbol tertentu, biasanya sebuah himpunan dinyatakan dengan menggunakan huruf besar/kapital seperti A, B, C, D, E, dst. atau bisa juga ditandai dengan adanya kurung kurawal, {…} sedangkan anggota dari himpunan tersebut biasanya ditandai dengan menggunakan huruf alfabet kecil seperti a,b,c,d,e, dst.

Untuk menyatakan sebuah himpunan, ada 4 buah cara yang bisa dilakukan. yaitu:

Enumerasi

Enumerasi adalah cara menyatakan himpunan dengan menuliskan seluruh anggota himpunan di dalam kurung kurawal. Setiap anggota di dalamnya dipisahkan dengan tanda koma. Misalnya: x = {s,a,p,i}

Simbol baku

Ada beberapa simbol tertentu yang sudah disepakati untuk menyatakan sebuah himpunan. sebagai contoh, simbol P biasanya digunakan utnuk menyatakan himpunan bilangan bulat positif, sedangkan huruf R digunakan untuk menyatakan sebuah himpunan yang berisi bilangan riil.

Notasi pembentukan himpunan

himpunan juga bis dinyatakan dengan cara menulis ciri-ciri umum dari anggota yang ada di dalam himpunan tersebut. misalnya: A = {x|x adalah himpunan bilangan riil}

Diagram venn

adalah cara menyatakan sebuah himpunan dengan menggambarkannnya dalam bentuk grafis. masing masing himpunan digambarkan dalam sebuah lingkaran dan dilingkupi olah himpunan semesta yang dinyatakan dalam bentuk persegi empat seperti pada gambar berikut:

Selain diagram venn, ada juga diagram garis dan diagram cartess, berikut penjelasannya:

Diagram garis

Diagram diatas menyatakan bahwa A dan B merupakan himpunan bagian dari C.

Diagram Cartes

Rene Descartes menjelaskan suatu himpunan dalam bentuk garis bilangan seperti gambar di bawah ini:

Macam-macam himpunan

ada beberapa jenis himpunan yang dikenal di dalam dunia matematika, yaitu:

Himpunan kosong

Himpunan kosong merupakan sebuah himpunan yang tidak ada anggota di dalamnya, biasanya jenis himpunan ini dituliskan dengan simbol ø atau { }.

Himpunan Semesta

adalah hmpunan yang memuat atau mencakup keseluruhan anggota yang sedang dibahah, iasanya himpunan ini ditandai dengan huruf S.

Himpunan bilangan

himpunan bilangan terdiri dari:

Himpunan terhingga

Himpunan terhingga adalah himpunan yang jumlah anggotanya masih terhingga, meliputi himpunan kosong dan himpunan yang memiliki n elemen. Contohnya:

X = {c, d, e, f} , Y = { }

Himpunan tak terhingga

Himpunan tak terhingga adalah himpunan yang jumlah anggotanya tidak terhingga. Comtohnya himpunan bilangan ganjil atau genap, himpunan bilangan bulat, dsb.

Operasi pada himpunan matematika

Sifat-sifat operasi pada himpunan matematika

Saya kira cukup sekian materi kali ini mengenai Pengertian, Teori, Konsep dan Jenis Himpunan Matematika sebenarnya masih ada pembahasan lanjutan mengenai himpunan matematika mungkin nanti akan saya lanjutkan pada artikel berikutnya.

http://www.rumusmatematikadasar.com/2014/09/pengertian-teori-konsep-dan-jenis-himpunan-matematika.html